Arbitrage as a Shortest Path Problem
An explanation of arbitrage and a look at an efficient algorithm to find riskless instantaneous arbitrage opportunities.
Who doesn’t like to make money?
And what if you could turn the problem of making money into the problem of finding the shortest-path? We can do that in at least one particular way: by exploiting arbitrage opportunities.
What is arbitrage?
Arbitrage is the act of buying or selling things across different markets, or in different forms, to profit from differences in prices. And the people who engage in it? They’re known as arbitrageurs — a fancy title indeed.
Let’s start with an example. Say Paul, Peter, and Bob live in a village, where they barter carrots, potatoes, and lettuce. Bob trades potatoes for carrots, Peter trades lettuce for potatoes, and Paul trades lettuce for carrots.
Furthermore, Bob will trade 2 potatoes for a carrot, Peter will trade 1 lettuce for 2 potatoes, and Paul will trade 2 carrots for 1 lettuce. If we were to treat each individual as a market for their respective goods, what would the exchange rates look like?
| Market | Exchange Rate |
|---|---|
| Bob (potatoes for carrots) | 2 potato/carrot |
| Peter (lettuce for potatoes) | 1 lettuce/2 potato = 0.5 lettuce/potato |
| Paul (carrots for lettuce) | 2 carrot/lettuce |
Exchange rates for goods in our village.
Do you sense an opportunity?
Being the enterprising individual that you are, you may try to exploit it. Starting with 5 carrots, you approach Bob, and trade your 5 carrots for 10 potatoes, at the rate at which he is willing to trade.
Next, you approach Peter with your potatoes, knowing that he’ll trade you 5 lettuce for them. Then you approach Paul with your 5 lettuce, and he trades 10 carrots for your lettuce.
After a few smart trades, you’ve doubled your carrot wealth. You turned 5 carrots into 10, by exploiting an arbitrage opportunity.
Later on, the villagers may develop more sophisticated markets where Bob, Peter, and Paul aren’t the only traders. Instead this little village might develop a carrot/lettuce market, a lettuce/potato market, and a potato/carrot market, where the going rate for each trade will fluctuate based on what people are willing to trade.
But the arbitrage principle remains the same. And the opportunity can be exploited until the traders offering to exchange at those rates run out of carrots, lettuce, and potatoes to trade. The arbitrage opportunity is exploited until the market reaches an equilibrium.
Arbitrage in Modern Times
When you think of modern markets, you probably don’t think of trading carrots, potatoes, and lettuce. If you’re into forex, you’re more likely thinking of trading dollars, pounds, and yen. And in that case, we would be dealing with a dollar/pound market, a pound/yen market, and a yen/dollar market, with many traders acting on each market. From now on, let’s use those currencies as examples of things to trade, but keep in mind the principles can apply to all sorts of trade-able things.
Say at a given time, the exchange rates are as follows:
| Market | Exchange Rate |
|---|---|
| pound (£) / dollar ($) | 0.8 pounds/dollar |
| yen (¥) / pound (£) | 100 yen/pound |
| dollars ($) / yen (¥) | 0.013 dollars/yen |
An example of currency market exchange rates.
If you learned anything from Bob, Peter, and Paul trading carrots, lettuce, and potatoes, you’d sense an opportunity here.
If you trade $1 for pounds, you’ll end up with £0.8. Trading that for yen, you’ll end up with ¥80. You take your yen to the yen/dollar exchange where you trade it back for dollars… but now you have $1.04!
But you have to act quickly, before another arbitrageur beats you to the punch. These opportunities only exist temporarily, until the liquidity is used up and the rates equalize.
The perceptive among you may notice that we haven’t considered exchange fees in our example. Of course, you’d have to take those into account to calculate if a profitable arbitrage opportunity actually exists.
Acting Quickly
Hopefully you have some intuition to understand why acting fast is paramount. Exchange rates fluctuate quickly, and there is only a limited amount of “thing” available at that exchange rate.
While we’ve worked with relatively simple examples here, arbitrage opportunities can span many trades, becoming incredibly complex. Our examples used 3 trades, but what if you needed 10? And in a network of 20 currencies with a market for each pair, how quickly could you find an opportunity?
Using a computer is an obvious answer. But we need an efficient algorithm, lest someone else beat us to the opportunity.
To achieve that, we can leverage a few clever insights in mathematics and computer science.
Markets as a Graph
Graphs are an incredibly important structure that has found its uses in numerous applications. Many social and natural structures can be modeled with graphs, and it turns out that markets are one of them.
In our case, let’s treat each currency as a node. Moving from node to node corresponds to trading one currency for another.
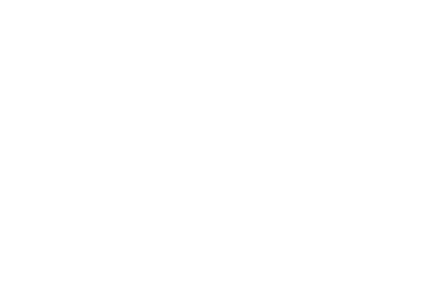
Simplified graph — there should be a distinct edge in each direction.
So moving along an edge, between nodes, should transform the amount of currency by the exchange rate.
That means moving from the dollar node to the pound node corresponds to multiplying by 0.8 pounds/dollar. Let’s assign the exchange rate as the weight of each edge.
Note that the exchange rate in each direction will be approximately the reciprocal of each other. That means if the rate to convert pounds to dollars is 0.8 pounds/dollar, the rate in the other direction will be 1/(0.8 pounds/dollar) = 1.25 dollars/pound. The consequence for us is that we need to be careful to treat buying and selling on each market as distinct, directed edges, with different weights.
The reason that the exchange rates in both directions are only approximately reciprocal is due to small differences in the prices to buy and sell currencies, known as the buy-sell spread. For example, if at a given moment you can buy pounds at 0.8 pounds/dollar (the current price somebody will sell to you), but can sell dollars for pounds at 0.82 pounds/dollar (or 1.22 dollars/pound, and the current price somebody will buy from you), your graph model will look like this (excluding the other exchange rates for simplicity):
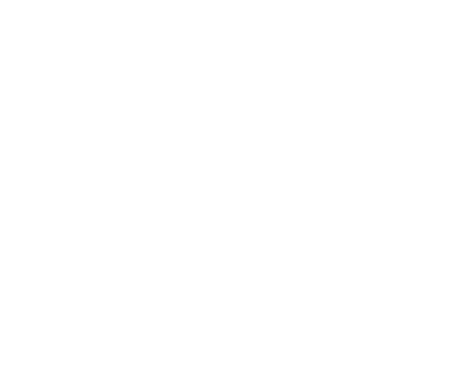
A series of trades can be modeled by moving along edges in this graph, and the result of the trades is computed by multiplying the edge weights as you move along them.
Seeing the Opportunity
Now that we have a working model, what are we looking for in our graph that corresponds to an arbitrage opportunity?
To determine whether a series of trades is profitable, we need a consistent metric of profitability. In other words, if we begin our series of trades in dollars, then we’ll need to end it in dollars, too. And by comparing the amount of dollars we ended up with to the amount we started with, we’ll know if it was profitable or not.
In our graph, that means that our series of trades must end at the same node from which it started. In our case, we started at the dollar node, and ended in the dollar node. In graph terminology, we call that a cycle. So we know we’re looking for some sort of cycle- but what kind of cycle makes it profitable?
Notice that if we multiply along the edges of a cycle, we transform the units of the effective exchange rate.
However, when we return to our starting node, the quantity becomes unit-less. It transforms from a rate of exchange, to a ratio of return! Traversing a cycle on our graph and computing the product of exchange rates along the way corresponds to calculating the ratio of return we would get after completing the series of trades.
If the market is perfectly efficient, our return ratio, \(abc\), will be 1, because the exchange rates have equalized. If the product of weights is greater than 1, say 1.02, then our arbitrage opportunity would have made us a 2% return.
Therefore, generalizing to an arbitrary number of trades, an arbitrage opportunity corresponds to the following inequality:
where \(e_i\) corresponds to the \(i^{th}\) exchange rate, for each trade \(i\), over n trades.
So what we need is an algorithm that will find a cycle on the graph of markets, where the product of edge weights is greater than 1. You might be able to invent an algorithm to do that - but in computer science, as in life in general, it’s useful to reduce problems to ones you already know how to solve.
The Bellman-Ford Algorithm
The problem of finding shortest paths is a common and fundamental problem in computer science, which can be applied to many different scenarios. An obvious one, by drawing a correspondence between a graph and a map, is that of finding the shortest route on a map. But with some cleverness, many other kinds of problems can be transformed into a shortest-path problem, as well. What I’m going to prove to you is that the problem of finding arbitrage opportunities is one such problem.
First, let’s establish what the shortest path problem is. Given two nodes in a graph, \(s\) and \(t\), the shortest path is that path which minimizes the sum of edge weights. In other words, we move along the path from \(s\) to \(t\), adding up edge weights along the way, the path with the minimum sum is the shortest path — the path with the smallest cost.
Next, it will be helpful to understand that there are different classes of shortest-path problems. In the obvious example — like the shortest route on a map — edge weights must be positive. There’s no way, barring a time machine, that driving down a road will reduce your travel time. In a graph with only positive edge weights, Dijkstra’s famous algorithm will compute the shortest path to all nodes in the graph.
However, there is no reason a graph cannot have negative edge weights. In that case, moving along that edge reduces the total cost of the path. But, if you have a cycle which has a negative weight, then you can keep traversing that cycle forever — every time, lowering your overall cost of the path — and your shortest path will have a cost approaching \(-\infty\). In that case, it would be very useful for our shortest-path algorithm to have a mechanism to identify negative weight cycles. Otherwise the shortest path would get stuck circling the negative weight cycle, forever.
The Bellman-Ford algorithm is exactly that algorithm. A more general version of Dijkstra’s shortest-path algorithm, it can handle negative weights. To do so, it detects negative weight cycles — cycles in a graph along which adding up the weights produces a negative value.
But how does an algorithm which can find cycles where the sum of edges is less than 0 help us, when we need an algorithm that can detect cycles where the product of edges is greater than 1?
Log to the Rescue
The next insight is that a product can be turned into a sum by applying the logarithmic function, thanks to the identity:
Thereby we can transform our problem of finding a cycle with a product greater than 1, to a problem of finding a cycle with a sum greater than 0! We do that by taking the log of each exchange rate, and using that as the weight of each edge.
Let’s show that by taking the log of both sides of our inequality. First, taking the log of the left-hand side transforms the problem of computing a product into computing a sum:
The log of the right side just transforms the 1 to a 0:
We’re close, but not quite there. The final step, to reduce our problem to one that we can solve with this known algorithm, is to multiply each edge weight by -1. This turns the problem of finding a positive weight cycle, into finding a negative one:
Which we know the Bellman-Ford algorithm can do! Constructing a graph as specified and executing the Bellman-Ford algorithm on it will quickly and efficiently find arbitrage opportunities for us, because we’ve turned the arbitrage problem into the problem of finding the shortest path — the infinitely shortest path.
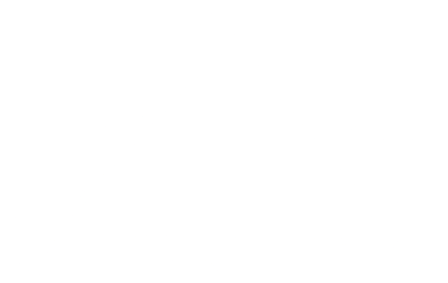
We need to find a negative weight cycle, where the weights are the negative logarithm of the exchange rates.
In hindsight, it’s obvious that there should be a correspondence between a negative weight cycle — which lowers the cost of the path every time you traverse it — to an arbitrage opportunity, which makes you a profit every time you traverse it. The key insight is transforming a problem of finding a product greater than 1 into finding a sum less than 0, by applying -log to the edge weights.
Prove It
Let’s run this algorithm on our exchange rates to see if it correctly identifies the arbitrage opportunity. Transforming the exchange rates by -log, we get:
| Market | -log(Exchange Rate) |
|---|---|
| pound (£) / dollar ($) | 0.223 |
| yen (¥) / pound (£) | -4.605 |
| dollars ($) / yen (¥) | 4.343 |
Summing over the trades, our equality holds- we found a negative weight cycle!
We can undo the logarithmic operation to restore the product, and calculate the return:
Which is exactly the 4% return we calculated earlier.
In the Real World
Since an arbitrage opportunity corresponds to a negative weight cycle, it seems that we could traverse the cycle forever to make infinite money. Of course, that is not the case.
The liquidity — the volume available before the price changes significantly- available for any arbitrage opportunity is limited, and is quickly exploited by algorithmic traders pushing the boundaries of computing technology and the laws of physics to beat each other.
That being said, I hope you found this exercise in applying graph theory and a well known shortest path algorithm to solving a problem in the finance domain — and making money — as interesting as I always have.